5.2.5 Affine transformations

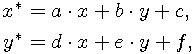
Every planar affine transformation

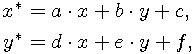
can be expressed as a square matrix such that

5.2.5.1 Transformation structure

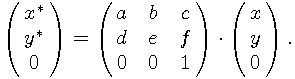
GEOMLIB stores transformation matrices in the structure

     struct geom_transform {
       uns flags;            /* special flags */
       real coef[2][3];      /* matrix coefficients */
     };

where

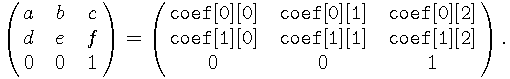
To speed up some operations with special cases of transformations, the flags entry may have set the following bits set:

GEOM_TRANSFORM_IDENTITY

Matrix expresses the identity transformation.

GEOM_TRANSFORM_SIMILAR

Matrix expresses a similarity.

These flags can be set up during the structure creation or manually by the user. There is no implemented numerical algorithm to detect similarities.

The list of implemented functions with a brief description can be found in the file geomlib/transform.h. There are functions to initialize the most useful affine transformations. The following routine is used to merge affine transformations:

     int geom_transform_merge(struct geom_transform *t1,
                              struct geom_transform *t2,
                              struct geom_transform *t);

Let T_1 and T_2 be matrices of some affine transformations. Then we can compute the matrix of the compound transformation by matrix multiplication 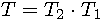. The code also sets the GEOM_TRANSFORM_IDENTITY and GEOM_TRANSFORM_SIMILAR flags in the resulting structure if they can be easily determined.

Another implemented methods are for example evaluations of the inverse matrix and the rank or detection of the fixed point of affine transformation.

5.2.5.2 Two-directional transformation structure

The following structure is used to optimize performance and increase the numerical stability of mixed manipulation with compound transformations and inversions.

     struct geom_transform2 {
       struct geom_transform primary; /* primary matrix */
       struct geom_transform inverted; /* inverse matrix */
     };

The header file geomlib/transform2.h defines operations similar to the operations in the file geomlib/transform.h, that work with this extended structure and update the inversion transformation matrix along with the primary matrix.