TIME parametrization may be generally [0, l], 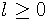 , but for elementary curves
it is restricted to unit interval [0, 1]. GEOMLIB includes direct conversion routines between
, but for elementary curves
it is restricted to unit interval [0, 1]. GEOMLIB includes direct conversion routines between
TIME and each other parametrization.
The item class extends o class by:
The group class extends item class by ordered set of child items. There are many routines for
manipulation with the set in the file geomlib/group.h. The implementation uses simple
circular linked lists, but it is prepared to be replaced by a balanced tree in the future development.
Single item may be inserted to at most one group at the time, so all existing items and groups generally form a set of trees (forest). Some of that trees are used in VRR Kernel (see Kernel) to describe hierarchy of geometrical objects (GOs) in top level objects (TLOs). For more detailed description of GEOMLIB grouping usage in the kernel, see kernel documentation. Other trees can be used for example as temporary paths.
Items and groups define a common interface abstract to all supported curves in plane. There are many virtual methods that must or may be redefined in derived classes.
To simplify addition of new curve types and geometrical routines to GEOMLIB there is only a small subset of required methods, that must be implemented in each descendant. If all of them are written correctly, other methods can be automatically emulated with a general code.
This mechanism is achieved by the following rules:
TIME) and parametrization of their Bézier expansion (BTIME).
When user calls a geometrical method without a special implementation, a general routine is executed.
At first, this method computes a Bézier expansion of the curve and converts all input TIME parameters to BTIME.
After that the geometrical task is solved by the code for paths and Bézier curves.
If there are curve parameters in the result, they are finally converted back from BTIME to TIME parametrization.
Some geometrical problems would be impossible to solve only by Bézier expansion and parametrization conversion routines. One of them would be the splitting of the curve in a given parameter to a pair of curves of the same type. In the current version of the VRR project, there are no such fully implemented functions, but they will probably appear in future releases.
For some curve types, the computation of Bézier expansions is quite slow in the majority of geometrical methods. To increase performance of repeated requests, entire expansion paths are stored in VRR 's cache. Full description of the caching mechanism can be found in the file geomlib/cache.c and Cache.
Implementation of the common curves interface is divided in the following files:
item class including abstract geometrical methods.
group class with ordered sets interface.
curve class definition (see Elementary curves).
Each curve can be expressed with infinite number of parametric forms. This is each continuous function from a real closed interval to the plane with the curve as the image. GEOMLIB defines four parametrizations for its curve types. Some of them may be identical.
TIME
This is the base parametrization for each type and is used in most of computations.
Therefore, its definition should allow the developer to implement a fast code.
Interval of TIME parametrization may be generally [0, l], 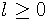 , but for elementary curves
it is restricted to unit interval [0, 1]. GEOMLIB includes direct conversion routines between
, but for elementary curves
it is restricted to unit interval [0, 1]. GEOMLIB includes direct conversion routines between
TIME and each other parametrization.
BTIME
BTIME is defined as TIME parametrization of the Bézier expansion. The interval is [0, n], where
n is the number of rational Bézier curves in the expansion.
ATIME
ATIME represents Euclidean arc length parametrization. The interval is [0, a], where a
is the Euclidean arc length of the curve. Parameter t corresponds to the point at the arc distance of t
from the starting point.
RATIME
RATIME is called relative Euclidean arc length parametrization.
This is exactly the previously defined ATIME parametrization linearly scaled to the unit interval [0, 1].
Full list of geometrical methods with brief description may be found in the file geomlib/item.h.
If a virtual method is called with prefix geom_item_, the correct function address from VMT is used.
Redefined virtual methods have prefixes according to the class name, for example geom_bezier_time_to_atime.
When we know exactly the class at the time of execution, we can use a little faster direct call to
the method instead of geom_item_ interface.