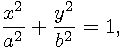
Implicit form of an ellipse with center in the origin and axis parallel to plane axis is
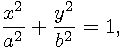
where a and b are lengths of the ellipse semi-axis.
Set of all general ellipses is a subset of all planar conics
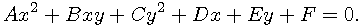
Planar conics include circles, ellipses, parabolas, hyperbolas and some degenerate cases (lines and points). Any of their finite sections can be replaced with a finite set of quadratic rational Bézier curves. GEOMLIB implements structures and direct manipulation with ellipses, circles and their sections. Other conic types are not supported fully.
The parametric form of general ellipse is
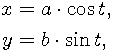
rotated around the origin and moved to the ellipse center point.
To store a section of ellipse (elliptic arc) we use this structure:
struct geom_elliptic_arc {
struct geom_curve curve; /* ancestor instance structure */
struct geom_point center; /* center point */
real rotation; /* rotation around the center point (CCW in radians) */
real a_radius; /* X-axis radius (a_radius >= 0) */
real b_radius; /* Y-axis radius (b_radius >= 0) */
real start; /* angle of arc starting point */
real dif; /* angle between endpoints */
};
The TIME parametrization with parameter s of the arc has the previously described parametric form,
where
We say that elliptic arc in parametric form is normalized if:
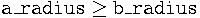
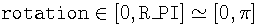
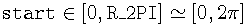
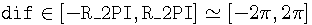
Every elliptic arc can be converted to this form. Almost every geometric routine assumes
a normalized elliptic arc as input and returns normalized arcs as its output.
Assertions of this required condition contain exact real constants for interval limits
and no rounding errors are allowed. The following function can be used to normalize a given elliptic arc:
int geom_elliptic_arc_normalize(struct geom_elliptic_arc *arc);
There are many routines that can be used to initialize entire ellipses in normalized form.
These are: the geom_elliptic_arc_set and all functions starting with geom_elliptic_arc_from_.
Full list with brief description can be found in geomlib/ellipse.h.
An elliptic arc can be created by one of these methods followed by a call to this function:
int geom_elliptic_arc_set_endpoints(
struct geom_elliptic_arc *arc, struct geom_point *start_point,
struct geom_point *end_point, struct geom_point *mid_point,
real start_angle, real dif_angle, uns flags);
The previous function computes start and dif entries in geom_elliptic_arc structure
by selected algorithm in the flags parameter. Meaning of remaining parameters depends on this value.
Input points should be near the ellipse. Resulting elliptic arc is always normalized.
The following example shows how to create an elliptic arc with given endpoints, rotation and eccentricity that pass through a given midpoint:
struct geom_elliptic_arc arc;
struct geom_point *start, *end, *mid;
real rotation, eccentricity;
/* ... compute input parameters */
/* instance creation */
geom_instance_init(&arc, GEOM_CLASS(elliptic_arc));
geom_elliptic_arc_create(&arc);
/* arc initialization */
if (GEOM_ETEST(geom_elliptic_arc_from_3_points_rotation_eccentricity(
&arc, start, end, mid, rotation, eccentricity)) &&
GEOM_ETEST(geom_elliptic_arc_set_endpoints(
&arc, start, end, mid, 0, 0, GEOM_CONIC_ARC_MIDDLE)) {
/* elliptic arc has been correctly initialized */
}
else {
/* floating point error */
}
/* instance destruction */
geom_elliptic_arc_destroy(&arc);
Expansion of elliptic arc to a set of quadratic rational Bézier curves is relatively simple.
We will describe a formula how to a convert circular arc of angle less than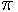 
.
General elliptic arc then can be expressed by at most three Bézier curves by applying
an affine transformation to converted circular arcs.
Let a circular arc has angle length 
. The following Bézier curve is exactly the same curve:
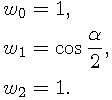
int geom_elliptic_arc_to_bezier(
struct geom_elliptic_arc *arc, struct geom_bezier *bezier);
int geom_elliptic_arc_expansion_append
(struct geom_elliptic_arc *arc, struct geom_fpath *expansion);
By the definition of implemented elliptic arcs, we only need to compute expansions of
unit circular arcs centered to the origin (at most 3 arcs) and then apply a scale (a_radius, b_radius),
rotation and translation (by center) to the result. There are some optimizations in the implementation, that
can be found in source code.
real geom_elliptic_arc_time_to_btime(struct geom_elliptic_arc *arc,
struct geom_expansion *expansion, real time);
To describe conversion from elliptic arc parametrization (t) to Bézier expansion parametrization (s), we assume, that
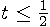and that there is only one Bézier curve in the expansion. Generalization to all possible cases would be simple.
The formula used for the computation is following:
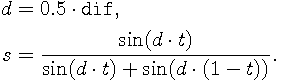
real geom_elliptic_arc_btime_to_time(struct geom_elliptic_arc *arc,
struct geom_expansion *expansion, real btime);
The reversed conversion for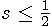 
is
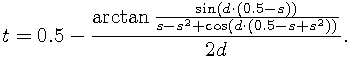
int geom_elliptic_arc_transform(struct geom_elliptic_arc *arc,
struct geom_transform *transform, struct geom_elliptic_arc *result);
Affine transformation of elliptic arc in previously defined parametric form is not an easy task. We have not discovered any direct formula for general transformation, so the computation is a little tricky. The curve is first converted to its implicit form where affine transformation can be applied. Finally, it is converted back to the resulting parametric form. These conversions can lead to numerical problems, especially for extremely thin and long ellipses or for almost singular transformations.
The long implementation of this algorithm, dealing with most of singularities, can be found in source geomlib/ellipse.c.