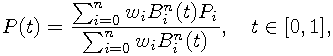
This is the most universal curve in GEOMLIB and any other supported curve can be converted to a finite sequence of rational Bézier curves. We have chosen rational Bézier curves to be the basic curve, because they can exactly represent both conic sections and
non-rational Bézier curves. They are also an equivalent to NURBS (non-uniform rational Bézier splines)
used in professional CAD systems.
General rational Bézier curve of degree n is represented by
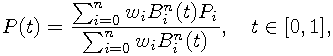
where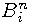 
are Bernstein basis polynomials, 
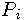are called control points and
scalars 
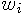are called weights. This definition describes used TIME (see TIME) parametrization of rational Bézier curves.
When all weights are the same, the equation can be rewritten to
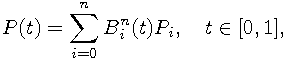
which is called non-rational Bézier curve or simply Bézier curve. This is equivalent to two-dimensional polynomial in Bernstein form (Polynomials in Bernstein form) with limited interval of the t parameter.
Another definition: A two-dimensional rational Bézier curve (x, y) is the three-dimensional non-rational Bézier curve (x, y, w) projected onto the plane w=1 by the central projection (division by w). This representation of projected three-dimensional space is called homogeneous coordinates.
GEOMLIB supports only limited degree of rational Bézier curves: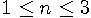 
. It is enough to describe
only the most useful curves. All weighs must be positive and to reach a good stability in numerical computations, weights should
not have extremely small or large values.
Data structures describing general rational Bézier curve are:
/* two-dimensional point with weight */
struct geom_point_w {
real x, y; /* coordinates */
real w; /* a positive weight */
};
/* rational Bézier curve */
struct geom_bezier {
struct geom_curve curve; /* ancestor instance structure */
struct geom_point_w pt[4]; /* control points and weights */
struct geom_rectangle bbox; /* cached bounding box */
real alength; /* cached Euclidean arc length */
};
Degree of the curve and flags are stored in the reserved bytes of geom_o header to minimize space requirement.
Possible flags are:
GEOM_BEZIER_NONRATIONALGEOM_BEZIER_BBOX_VALIDGEOM_BEZIER_ALENGTH_VALIDThe geometrical meaning of some rational Bézier curves is:
To split non-rational Bézier curves at a given parameter t, we implemented the de Casteljau algorithm.
Output is the pair of non-rational Bézier curves, that correspond to subintervals [0, t] and
[t, 1] of the original curve.
The TIME parametrizations of resulting curves are preserved and only scaled from subintervals back to unit interval.
/* Splits rational Bézier curve at TIME parameter 0.5. */
int geom_bezier_split_middle(struct geom_bezier *bezier,
struct geom_bezier *left, struct geom_bezier *right);
/* Splits rational Bézier curve at a given TIME parameter. */
int geom_bezier_split_at(struct geom_bezier *bezier,
real time, struct geom_bezier *left, struct geom_bezier *right);
Let 
are the control points of non-rational Bézier curve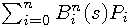 
.
Then we define:
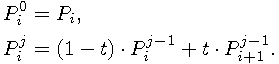
Resulting curve for parameter subinterval [0, t] has control points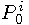 
and for
[t, 1] control points 
.
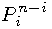Rational Bézier curves can be split in homogeneous coordinates by the same algorithm.
The described algorithm can be used multiple times to split the curve to a sequence of very small curves. By reducing length of the subintervals, the resulting curve parts convert to short segments with linear parametrizations. This property allows us to solve problems, that would be very hard or impossible to solve directly. One of such problems is computation of Euclidean arc length, which is impossible to solve exactly for rational Bézier curves in the algebraic way.
It is better to implement iterative splits by recursive subdivision in the half, than many splits at smaller parameter values. Recursive subdivision of Bézier curves is known to be numerically stable and we can locally control number of splits, according to the current part's shape.
There are more interfaces to recursive subdivision in GEOMLIB. The following example describes one of them:
struct geom_bezier bezier; /* rational Bézier curve to subdivide */
struct geom_bezier_subdivision sub; /* temporarily structure */
/* ... */
/* initialize the subdivision */
geom_bezier_subdivision_init(&sub, &bezier);
/* main subdivision cycle */
while (geom_bezier_subdivision_next(&sub)) {
/* if bezier curve sub.bezier is "small" enough... */
if (...) { /* subdivision condition */
/* ... then use it */
}
/* else split it recursively */
else
geom_bezier_subdivision_split(&sub);
}
/* clean up temporarily data */
geom_bezier_subdivision_destroy(&sub);
Information in the subdivision structure, that may be used in the condition is:
struct geom_bezier_subdivision {
struct geom_bezier *bezier; /* pointer to current subdivided part */
uns depth; /* recursion depth */
real left; /* left limit of current interval */
real right; /* right limit of current interval */
/* ... internal data entries */
};
More detailed description of subdivision interfaces can be found in the file geomlib/bezier.h.
int geom_bezier_point_at_time(struct geom_bezier *bezier,
real time, struct geom_point *result);
The previous routine evaluates P(t) from rational Bézier curve definition. Implementation calls de Casteljau algorithm to split the curve and returns common control point of split curves (endpoint interpolation property of rational Bézier curves).
int geom_bezier_derivation_at_time(struct geom_bezier *bezier,
real time, struct geom_vector *result);
The previous function applies tangency condition of rational Bézier curves to evaluate requested derivation vector. The curve is split at the parameter and derivation in endpoint of one part scaled by its interval size is returned. Following equations are equivalent and the one with better numerical stability (larger interval) is chosen:
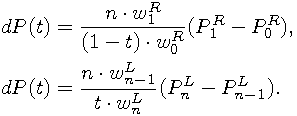
/* Computes Euclidean arc length of a given rational Bézier curve. */
real geom_bezier_alength(struct geom_bezier *bezier)
/* Conversions between TIME and ATIME parametrizations. */
real geom_bezier_time_to_atime(struct geom_bezier *bezier, real time);
int geom_bezier_times_to_atimes(struct geom_bezier *bezier,
uns count, real *times, real *atimes);
real geom_bezier_atime_to_time(struct geom_bezier *bezier, real atime);
int geom_bezier_atimes_to_times(struct geom_bezier *bezier,
uns count, real *atimes, real *times);
For rational Bézier curves, it is generally impossible to express Euclidean arc length and TIME–ATIME (ATIME) conversions
by an expression. Even for elliptic arcs (a subset of quadratic rational Bézier curves), there appear
nontrivial elliptic integrals that are usually solved by iterative methods. Non-rational Bézier curves
cause problems from third degree.
To solve these problems, we apply recursive subdivision to approximate the curve by segments and to compute arc length of the resulting polygon. All listed routines use the same approximation to almost straight parts with almost linear parametrizations, so mixed calls should have good behaviour. If we need to convert several parameters at one time, it is much more effective to call only one routine with all the parameters (single subdivision). If the arc length is computed it is stored in Bézier structure cache for later reuse.
More details about the implementation can be found in the file geomlib/bezier_param.c.
This function finds the TIME parameters, where the first derivation is parallel to a given vector.
In situations with zero of infinite number of solutions, function returns no result.
int geom_bezier_direction_times(struct geom_bezier *bezier,
struct geom_vector *vector, uns flags, double *result);
Without loss of generality we can assume, that the direction vector is parallel to x axis. If it is not, we apply a linear transformation to the vector and curve.
The curve is parallel to x axis only when the partial derivation in y is zero. For rational Bézier curve we get
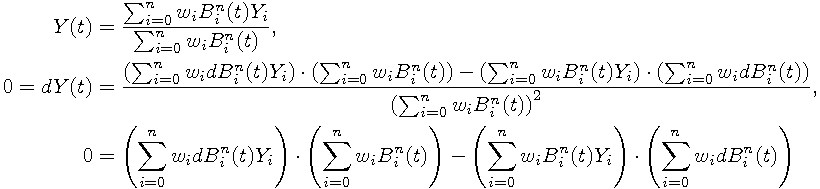
and for non-rational curves
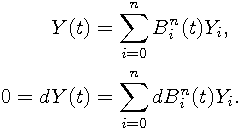
All we need is derivation, multiplication and subtraction of Bernstein polynomials and a general root solver. These routines are defined in geomlib/bernstein.h. Some special cases are computed directly to increase the performance. Functions are implemented in geomlib/bezderiv.c.
The problem is similar to finding a bounding box of these points:
int geom_bezier_bbox(struct geom_bezier *bezier,
struct geom_rectangle *result);
The previous function calls geom_bezier_direction_times twice to retrieve the interior points and
returns their common bounding box with the first and last control point. In some singular cases,
the algorithm can fail to find the correct bounding box.
This function finds all TIME parameters, where the curve is at a given distance to a given point.
int geom_bezier_distance_times(struct geom_bezier *bezier,
struct geom_point *point, real distance, struct garr *result);
Without loss of generality, we can assume that the point is located in the origin. Otherwise, we can translate the curve. Let the desired distance is D. For rational Bézier curve we get
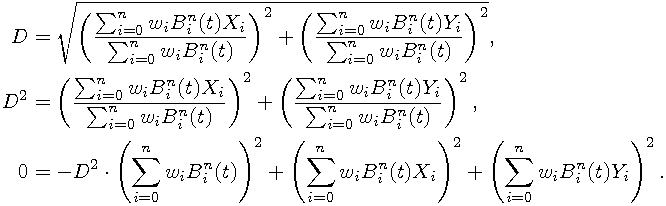
To solve roots of this polynomial, we can use routines from geomlib/bernstein.h. See geomlib/beznear.c for implementation details.
int geom_bezier_nearest_to_point(struct geom_bezier *bezier,
struct geom_point *point, uns flags, struct geom_nearest *result);
Without loss of generality, we can assume, that the point is located in the origin. Otherwise, we can translate the curve. Problem is similar to finding the nearest points of these:
The second set of points can be described by
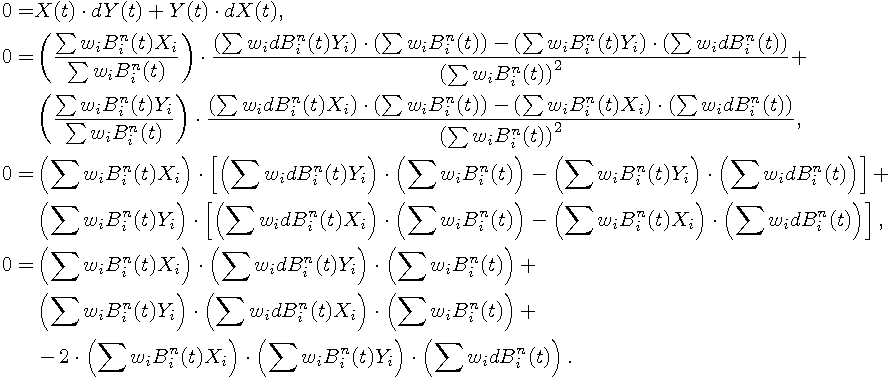
All sums are from zero to n. The resulting polynomial is of degree eight for rational cubic curves,
but most cases are much easier. Main parts of the implementation can be found in the internal
function geom_bezier_center_extreme_times in geomlib/beznear.c.
The algorithm can miss the correct nearest point in some singular cases.
int geom_beziers_intersections(struct geom_bezier *bezier1,
struct geom_bezier *bezier2,
uns flags, struct garr *result);
Computing all intersections of two rational Bézier curves is one of the most difficult tasks in GEOMLIB and it could be improved in many ways in the future. Usually, the problem is solved by recursive subdivision, polynomial solver or algorithms dealing with eigenvalues. Because there is a general polynomial solver implemented in the project, we have chosen the polynomial way.
Implemented algorithm is inspired by the article D. Machota, J. Demmel: Algorithms for Intersecting Parametric and Algebraic Curves I: Simple Intersection. In this text the problem of computing intersections of rational curves (in parametric or implicit form) is reduced to eigenvalue problem, but some ideas can be easily adapted for the usage of the polynomial solver.
Let P(t) be the first input curve and Q(s) the second one. The main idea is to convert Q(s) to implicit form F(x, y)=0, substitute first curve P(s) to obtain an univariate polynomial and call polynomial solver to get the intersection parameters on the first curve. Finally, if it is necessary, points and parameters on the second curve are evaluated.
Detailed description of rational Bézier curve implicitization can be found in the cited article. The algorithm results in symbolic matrix (each entry is a linear combination of 1, x and y), whose determinant is the curve in implicit form F(x, y)=0.
Before the implicitization is performed, the algorithm tries to reduce curve degree while preserving curve shape to avoid zero determinant of implicit matrix. Such curve is for example non-rational quadratic Bézier curve with the middle control point in the center of the others.
The rest of algorithm is simple, provided we have implemented polynomial solver, curve points evaluation and algorithm for finding nearest points. Details can be found in geomlib/bezinter.c. In some special cases, the algorithm fails to find the intersections.
int geom_bezier_elevate(struct geom_bezier *bezier,
uns target_degree, struct geom_bezier *result);
Degree elevation of a rational Bézier curve means to increase the number of control points while preserving curve shape and parametrization. This can be done exactly in the algebraic way. Used formulas and implementation details can be found in geomlib/bezier.c.
The previous function is extensively used while exporting images to PS, PDF and SVG (see Export) to convert lower degree curves to cubic Bézier curves.