5.2.2 Polynomials in Bernstein form

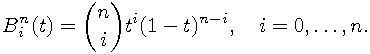
The n+1 Bernstein basis polynomials of degree n are defined as

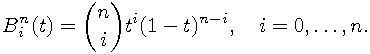
A linear combination of Bernstein basis polynomials,

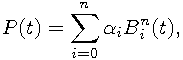
is called a Bernstein polynomial or polynomial in Bernstein form of degree n. The coefficients 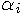are called Bernstein coefficients or Bézier coefficients. Every polynomial in power form can be written in Bernstein form and vice-versa.

GEOMLIB widely use Bernstein polynomials because the base curve type (Rational Bezier curves) contains Bernstein basis polynomials in its definition. The file geomlib/bernstein.h defines routines similar to the routines in geomlib/polynomial.h to solve the polynomials in Bernstein form and conversion routines between power and Bernstein form. There are also another useful operators such as multiplication, addition or derivation of the polynomials.

Implementation of the Bernstein polynomial solver is very simple. It converts the polynomial to power form and then executes previously described solver (see Polynomials in power form). In some situations (especially in higher degrees) it would be more effective and geometrically stable to solve Bernstein polynomials and Bézier curve problems with specialized algorithms, but it is left for the future development of VRR project.

The most important functions in the header file geomlib/bernstein.h are:

     /* Conversion of a given polynomial from Bernstein form to power form. */
     int geom_bernstein_to_power(uns degree, double *bernstein, double *power);
     
     /* Conversion of a given polynomial from power form to Bernstein form. */
     int geom_power_to_bernstein(uns degree, double *power, double *bernstein);
     
     /* Finds all roots of a given polynomial in Bernstein form.
        Meaning of flags is the same as in geom_polynomial_solve. */
     int geom_bernstein_solve(uns degree, double *coef,
                              uns flags, double *result);