5.2.1 Polynomials in power form

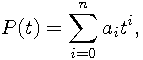
GEOMLIB contains a general polynomial solver which is used in most of curves computations (see Rational Bezier curves).

The power form of the general polynomial P(t) is

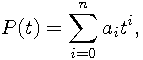
where:

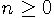• is called the degree of the polynomial.
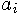• are called the coefficients of the polynomial.
• n=0 or .

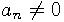Each nonzero polynomial of degree n has at most n real roots (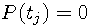). The following function finds all these roots in the increasing order:

     int geom_polynomial_solve(uns degree, double *coef,
                               uns flags, double *result);

To achieve a good numerical stability, all computations work in the double precision. Possible options to the algorithm can be passed in flags parameter as an OR combination of the following bits:

GEOM_SOLVE_LEFT_ONLY

Returns only the minimal root if exists.

GEOM_SOLVE_UNIT_INTERVAL

Returns only the roots in the closed interval [0, 1].

GEOM_SOLVE_MULTIPLICITY

Returns each root with multiplicity k as k identical entries in the resulting array.

We have implemented closed form solvers up to degree 4 (including), because they are faster then the general iterative solver designed for higher degrees. Mathematical basis of these algorithms can be found at http://mathworld.wolfram.com/ (Cubic Equation, Quartic Equation).

Roots of the degree 5 or higher polynomials can be found with Jenkins-Traub iterative algorithm. We have translated the C++ implementation from http://www.crbond.com/ to C99 standard. Detailed description of the algorithm is beyound the scope of this documentation, but some brief comments can be found in the source file geomlib/polynomial.c.